Integers on number lines

Integers on number lines by Delta publications

Key Notes:

🔷 1. What are Integers?

Integers are whole numbers that can be:

  • Positive (e.g., +1, +2, +3)
  • Negative (e.g., -1, -2, -3)
  • Zero (0)

📌 Set of Integers: {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

In Maths, number lines are the horizontal straight lines in which the integers are placed in equal intervals. All the numbers in a sequence can be represented in a number line. This line extends indefinitely at both ends. 

 Every real number is represented by a unique point on the Number line. Also, every point on a number line represents one & only one Real number. We use the process of successive magnification to represent a number on number line.

🔷 2. Understanding the Number Line

A number line is a horizontal line used to show the position of integers.

    ←––––––––––––––––––––––––––––––––––––––––––→
   -5  -4  -3  -2  -1   0   1   2   3   4   5
Integers on number lines

You can plot integers on number lines. On a number line, negative integers are to the left of zero, and positive integers are to the right of zero.

Let’s try it. Plot 2 on the integer number line. The integer 2 is positive, so it is to the right of zero.

A number line from -5 to 5, counting by 1s, is shown. There is a point on the number line at 2.

Let’s try it for another example. Plot –4 on the integer number line. The integer –4 is negative, so it is to the left of zero.

A number line from -5 to 5, counting by 1s, is shown. There is a point on the number line at -4.
✅ Key Points:
  • 0 is the center point.
  • Numbers increase to the right.
  • Numbers decrease to the left.
  • Every number has a fixed distance from 0 called its absolute value.
🔷 3. How to Plot Integers on a Number Line

✏️ Steps to plot:

  • Draw a straight line and mark equal intervals.
  • Label 0 at the center.
  • Mark positive numbers to the right.
  • Mark negative numbers to the left.
  • Use dots or circles to plot specific numbers.

📝 Example: Plot -3 and +4

cssCopyEdit←––––––––––––––––––––––––––––––––––––––––––→
   -5  -4  [-3]  -2  -1   0   1   2   3  [4]  5
🔷 4. Comparing Integers Using the Number Line

📚 Remember:

  • The number on the right is always greater.
  • The number on the left is always smaller.

💡 Examples:

  • 3 > -2 ✅ (Because 3 is to the right of -2)
  • -5 < -1 ✅ (Because -5 is to the left of -1)
🔷 5. Real-Life Examples of Integers
  • 📉 Temperatures: -10°C (cold), +30°C (hot)
  • 🏦 Bank balance: -₹500 (debt), +₹500 (savings)
  • 🎮 Game scores: +20 (win), -10 (loss)
  • 🏔️ Altitudes: +200 m (above sea level), -50 m (below sea level)
🔷 6. Practice Time! ✍️

Try these on your own:

  • Plot: -5, -1, 0, 2, 4 on a number line.
  • Compare:
    a) -2 __ 1
    b) -6 __ -3
    c) 0 __ -7
  • Which number is between -3 and 2?
  • Which is greater: -4 or -5?
  • On the number line, which number is farthest from 0: -6, 4, or -8?
📌 Quick Tips:
ConceptRule
Right of number lineGreater value
Left of number lineSmaller value
Closer to 0Smaller absolute value
ZeroNeither positive nor negative
Same distance from 0Opposites (e.g., -3 and +3)

Learn with an example

➡️ Type the missing number.

  • Each interval represents 1, so find the missing number by adding or subtracting 1.
  • The missing number is larger than –3, so add 1. Since –3 + 1 = –2, the missing number is –2.

➡️ Type the missing number.

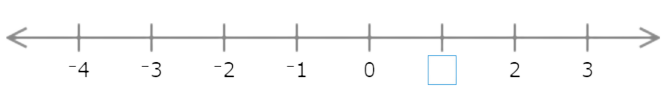
  • Each interval represents 1, so find the missing number by adding or subtracting 1.
  • The missing number is larger than 0, so add 1. Since 0 + 1 = 1, the missing number is 1.

🔥Type the missing number.

  • Each interval represents 1, so find the missing number by adding or subtracting 1.
  • The missing number is larger than –1, so add 1. Since –1 + 1 = 0, the missing number is 0.

Try some practice problems!