Identify rational numbers
Key notes:
🔢 What is a Rational Number?
A rational number is any number that can be written in the form a/b, where:
- a = integer
- b = integer (but not zero)
👉 Example: 3/4, −5/2, 7, 0
🧮 Integers are Rational Numbers
All integers like −3, 0, 12 can be written as a fraction:
-3 = -3/1
12 = 12/1
✨ So, all integers are rational numbers.
💡 Decimals can be Rational Numbers
Decimals that are:
- Terminating (end after few digits) like 2.5, 6.75
- Repeating like 0.333…
👉 These can be converted into fractions, so they are rational numbers ✨
🚫 What is NOT a Rational Number?
Numbers that cannot be written as a fraction are irrational numbers:
❌ √2
❌ π
❌ 0.101001000… (non-repeating, non-terminating decimal)
🧀 Rational Numbers on a Number Line
Rational numbers can be placed on the number line just like whole numbers.
👉 Example: 1/2 lies between 0 and 1.
📍 Every rational number has a exact position on the number line.
🎯 Rational Numbers Include:
✔ Positive numbers
✔ Negative numbers
✔ Zero
✔ Fractions
✔ Decimals (terminating/repeating)
🔍 Quick Test to Identify a Rational Number
Ask:
👉 Can I write it as a/b?
If yes → Rational number 😊
If no → Irrational number 🚫
🌈 Examples of Rational Numbers
- 4 = 4/1
- −7/9
- 0.75 = 3/4
- 0 = 0/1
- 2.222… = 2 2/9
🎉 Fun Fact!
Every rational number has many equivalent forms.
Example:
1/2 = 2/4 = 3/6 = 50/100 🌟
Learn with an example
🗼Is –2 a rational number?
- yes
- no
-2 can be written as -2/1, which is a fraction. So, -2 is a rational number
🗼 Is –10 a rational number?
- yes
- no
-10 can be written as -10/1, which is a fraction. So, -10 is a rational number
🗼 Is 5 a rational number?
- yes
- no
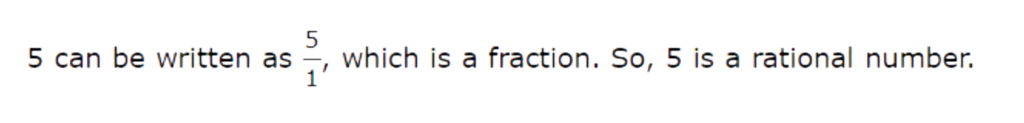
5 can be written as 5/1, which is a fraction. So, 5 is a rational number
Let’s practice!🖊️

