Multiply and divide rational numbers

Key notes:

1. What are Rational Numbers?

  • A rational number is any number that can be expressed as the ratio of two integers, i.e., in the form a/b, where:
    • a and b are integers
    • b ≠ 0
    • Examples: 1/2, -3/4, 5, -7, 0.75 (which is 3/4), etc.

2. Multiplying Rational Numbers

  • Rule for Multiplying Rational Numbers:
    • Multiply the numerators together.
    • Multiply the denominators together.
    • Simplify the resulting fraction if possible.
  • Signs of the Product:
    • If both numbers have the same sign (both positive or both negative), the product is positive.
    • If the numbers have opposite signs, the product is negative.

3. Dividing Rational Numbers

  • Rule for Dividing Rational Numbers:
    • Multiply the first rational number by the reciprocal of the second rational number.
    • The reciprocal of a fraction a/b is b/a (swap the numerator and denominator).
  • Signs of the Quotient:
    • If both numbers have the same sign, the quotient is positive.
    • If the numbers have opposite signs, the quotient is negative.

Learn with an example

🗼 Multiply. – 3 1/4 x 1 3/5 = _____

  • Write the mixed numbers as improper fractions.

– 3 1/4 x 1 3/5

– 13/4 x 8/5

  • Cancel common factors, then multiply.

– 13/4 x 8/5 = – 13/1 x 2/5

= – 13 x 2 / 1 x 5

= 26 / 5

  • Simplify the answer.
  • – 26/5 = – 5 1/5

🗼 Multiply. – 1/2 x 1 1/2 = ____

  • Write the mixed number as an improper fraction.
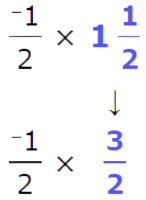
  • Now multiply.

– 1/2 x 3/2 = – 1 x 3 / 2 x 2

= – 3 / 4

🗼 Multiply. 1/8 x 2 = _____

  • Write the whole number as a fraction.
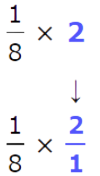
  • Cancel common factors, then multiply.

1/8 x 2/1 = 1/4 x 1/1

= 1 x 1 / 4 x 1

=1/4

Let’s practice!🖊️