Use Venn diagrams to solve problems
Learn with an example
🔔 Of the people on Evelyn’s street, 9 have been to Boise and 5 have been to San Diego. 3 people have been to both Boise and San Diego. How many people have been to Boise or San Diego or both?
_____ people
Make a Venn diagram to solve the problem.
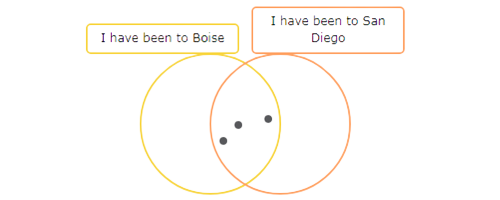
3 people have been to both Boise and San Diego. Put 3 dots in the area that is in both circles.
Now add dots to the other two areas until there are 9 dots in the “I have been to Boise” circle and 5 dots in the “I have been to San Diego” circle.
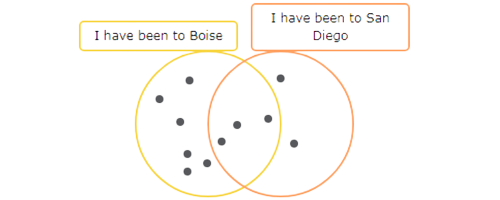
Count the total number of dots in the diagram. There are 11 dots.
11 people have been to Boise or San Diego or both.
🔔 Of the children in Braden’s class, 8 like to use markers. 9 children like to use chalk. 4 children like to use both markers and chalk. How many children like to use markers or chalk or both?
_____ children
Make a Venn diagram to solve the problem.
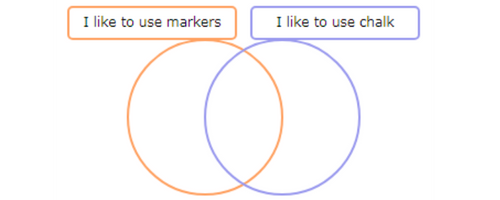
4 children like to use both markers and chalk. Put 4 dots in the area that is in both circles.
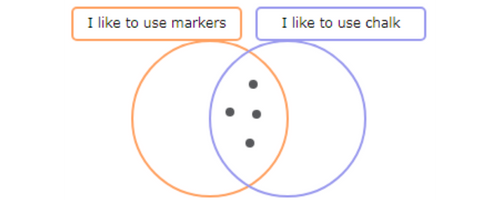
Now add dots to the other two areas until there are 8 dots in the “I like to use markers” circle and 9 dots in the “I like to use chalk” circle.
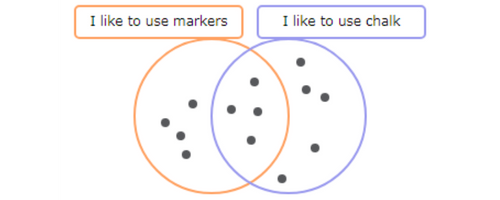
Count the total number of dots in the diagram. There are 13 dots.
13 children like to use markers or chalk or both.
🔔 8 of the students in Keenan’s class like to eat crackers and 4 like to eat crisps. 3 students like to eat both crackers and crisps. How many students like to eat crackers or crisps or both?
_____ students
Make a Venn diagram to solve the problem.
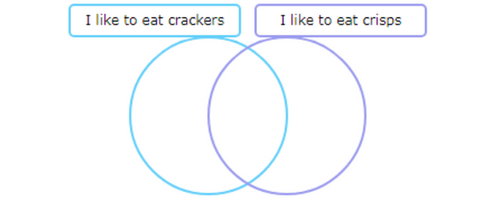
3 students like to eat both crackers and crisps. Put 3 dots in the area that is in both circles.
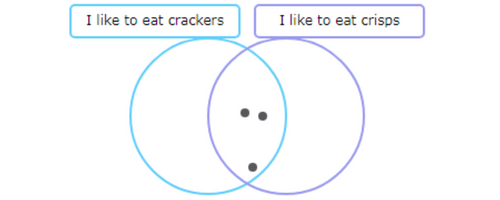
Now add dots to the other two areas until there are 8 dots in the “I like to eat crackers” circle and 4 dots in the “I like to eat crisps” circle.
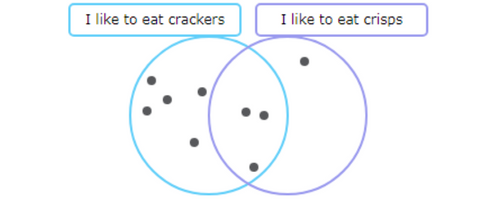
Count the total number of dots in the diagram. There are 9 dots.
9 students like to eat crackers or crisps or both.
Let’s practice! 🖊️

