Interior angles of polygons
Key notes:
Interior Angles of Polygons
- Definition of Polygons:
- A polygon is a closed figure formed by three or more straight line segments (sides) that do not cross each other.
- Types of Polygons:
- Regular Polygons: All sides and angles are equal (e.g., equilateral triangle, square).
- Irregular Polygons: Sides and angles are not all equal (e.g., trapezoid, rectangle).
- Interior Angles:
- The interior angles are the angles formed inside a polygon at each vertex where two sides meet.
- Sum of Interior Angles:
- The sum of the interior angles of a polygon can be calculated using the formula: Sum of interior angles=(n−2)×180° where n is the number of sides in the polygon.
Learn with an example
📢 What is the sum of the angle measures in this shape?
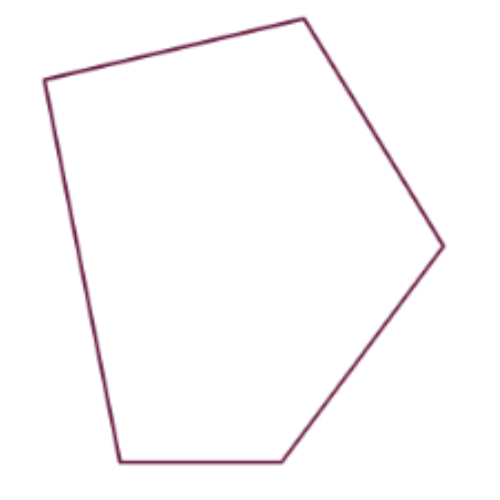
____°
Find out how many triangles make up a pentagon.

A pentagon is made up of 3 triangles, which each have 180°. Multiply.
3 × 180° = 540°
The angle measures of a pentagon add up to 540°.
📢 What is the sum of the angle measures in this shape?
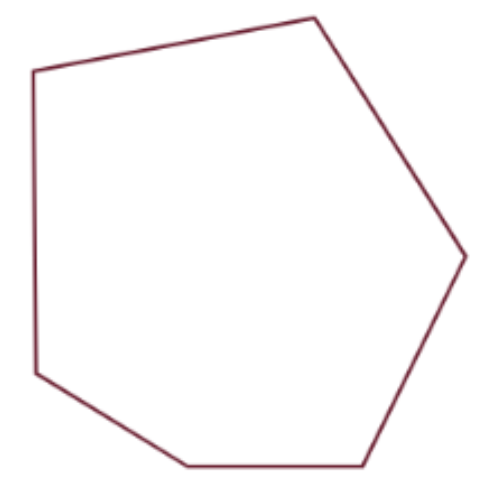
_____°
Find out how many triangles make up a hexagon.
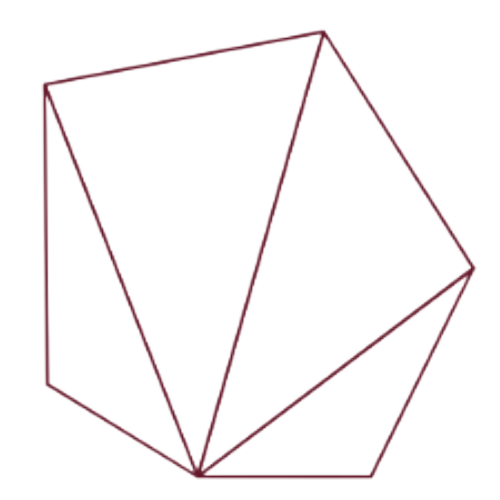
A hexagon is made up of 4 triangles, which each have 180°. Multiply.
4 × 180° = 720°
The angle measures of a hexagon add up to 720°.
📢 What is the sum of the angle measures in this shape?
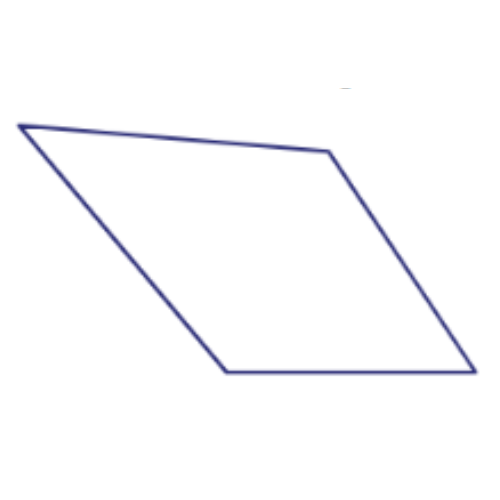
______°
Find out how many triangles make up a quadrilateral.
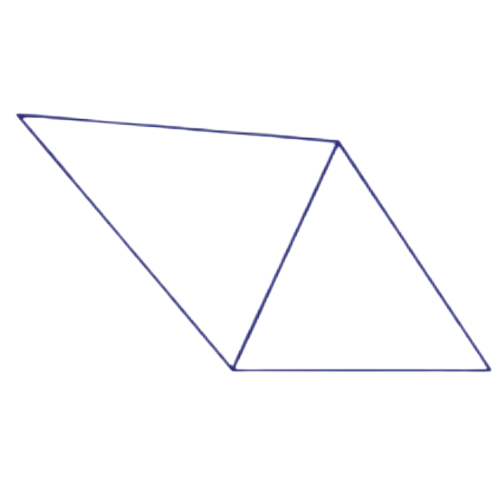
A quadrilateral is made up of 2 triangles, which each have 180°. Multiply.
2 × 180° = 360°
The angle measures of a quadrilateral add up to 360°.
Let’s practice!🖊️

