Find measures of complementary, supplementary, vertical and adjacent angles
Key notes:
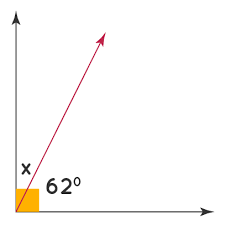
1. Complementary Angles
- Definition: Two angles are complementary if the sum of their measures equals 90 degrees.
- Example: If one angle measures 30 degrees, the other angle must measure 90−30=60 degrees.
- Visualization: Often represented as two angles that form a right angle (90 degrees) when combined.
2. Supplementary Angles
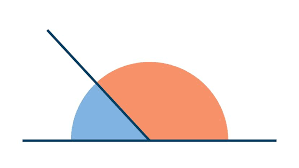
- Definition: Two angles are supplementary if the sum of their measures equals 180 degrees.
- Example: If one angle measures 110 degrees, the other angle must measure 180-110=70 degrees.
- Visualization: Often represented as two angles that form a straight line (180 degrees) when combined.
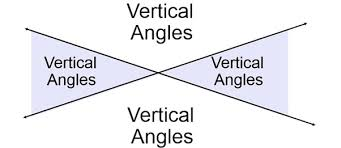
3. Vertical Angles
- Definition: Vertical angles are the angles opposite each other when two lines intersect. They are always equal in measure.
- Example: If two lines intersect and one angle measures 50 degrees, the angle directly opposite it also measures 50 degrees.
- Visualization: Formed by the “X” shape created by two intersecting lines.
4. Adjacent Angles
- Definition: Adjacent angles are two angles that share a common side and a common vertex but do not overlap.
- Example: In a shape with four angles, if one angle is 45 degrees and shares a side with another angle, they are adjacent.
- Visualization: Often seen in polygons, such as quadrilaterals, where angles are next to each other.
Learn with an example
📢 What is the value of h?
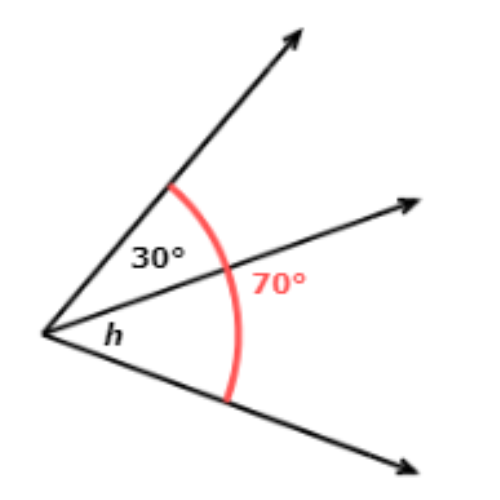
_______°
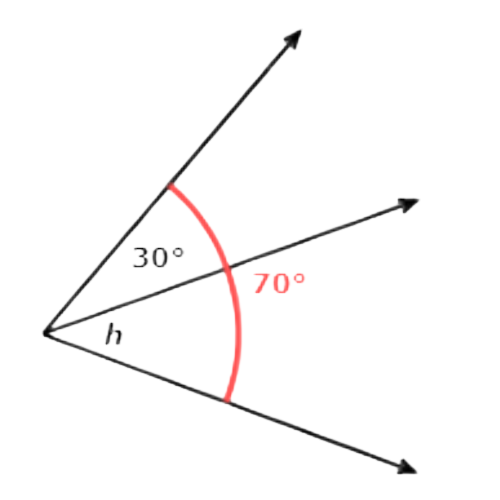
Add the measures of the adjacent angles and set the sum equal to 70°. Then solve for h.
30° + h = 70°
h = 70° − 30°
h = 40°
So, h = 40°.
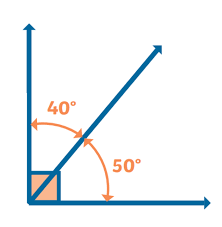
📢 What is the value of q?
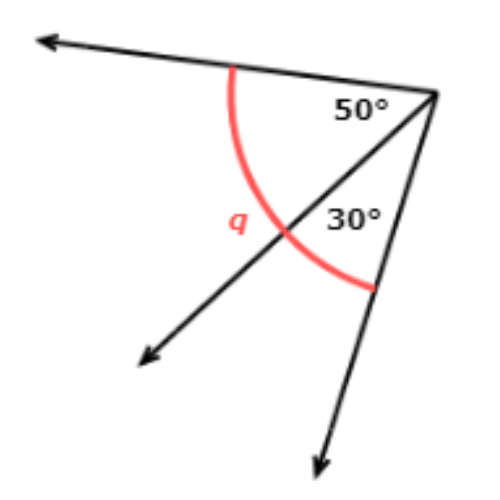
_____°
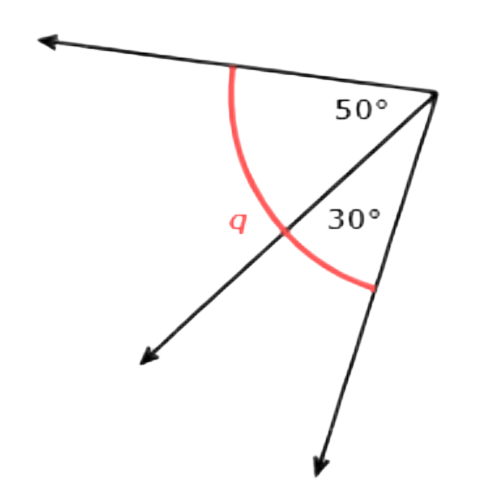
Add the measures of the adjacent angles.
q = 30° + 50°
q = 80°
So, q = 80°.
📢 What is the value of j?
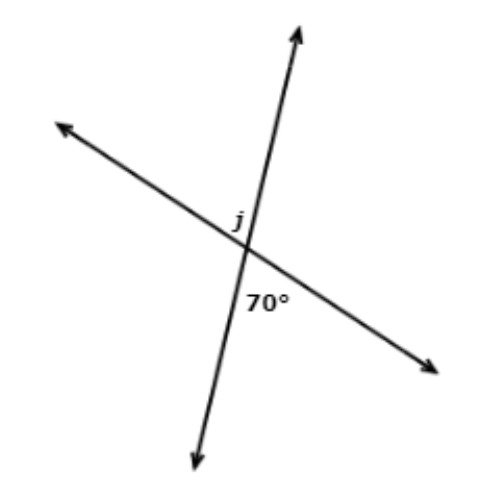
_______°
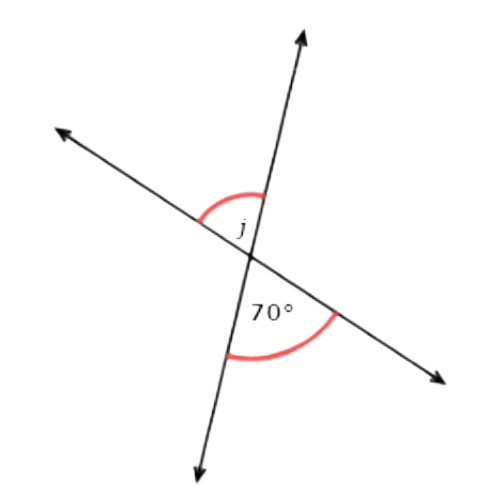
Vertical angles are congruent, so they have the same measure.
So, j = 70°.
Let’s practice!🖊️

