Transversal of parallel lines

Key notes:

  1. Definition of a Transversal:
    • A transversal is a line that crosses two or more lines at distinct points.
  2. Parallel Lines:
    • Parallel lines are lines in the same plane that never intersect. They maintain a constant distance apart.
  3. Angles Formed by a Transversal:
    • When a transversal intersects parallel lines, several types of angles are formed:
      • Corresponding Angles: Angles in the same position at each intersection. They are equal.
      • Alternate Interior Angles: Angles on opposite sides of the transversal and inside the parallel lines. They are equal.
      • Alternate Exterior Angles: Angles on opposite sides of the transversal and outside the parallel lines. They are equal.
      • Consecutive Interior Angles: Angles on the same side of the transversal and inside the parallel lines. Their measures add up to 180° (they are supplementary).

Properties of Angles with Transversals

  • Corresponding Angles Postulate: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
  • Alternate Interior Angles Theorem: If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
  • Alternate Exterior Angles Theorem: If a transversal intersects two parallel lines, then each pair of alternate exterior angles is equal.
  • Consecutive Interior Angles Theorem: If a transversal intersects two parallel lines, then each pair of consecutive interior angles is supplementary (adds up to 180°).

Learn with an example

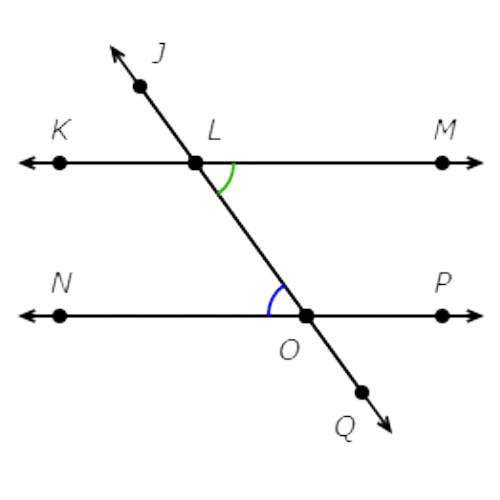
🔔 KM and NP are parallel lines.

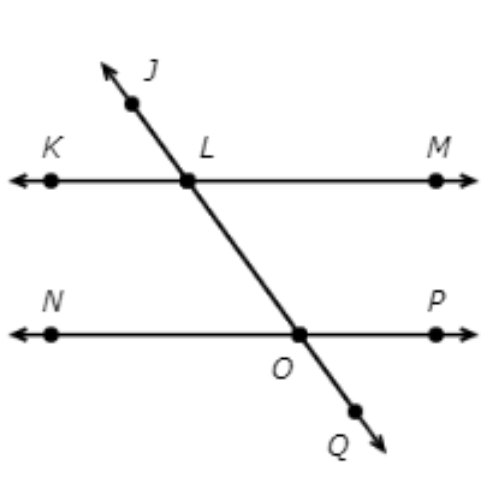
Which angles are alternate interior angles?

  • ∠NOL and ∠NOQ
  • ∠NOL and ∠MLO
  • ∠NOL and ∠POQ
  • ∠NOL and ∠KLJ

The transversal is JQ

First find ∠NOL.

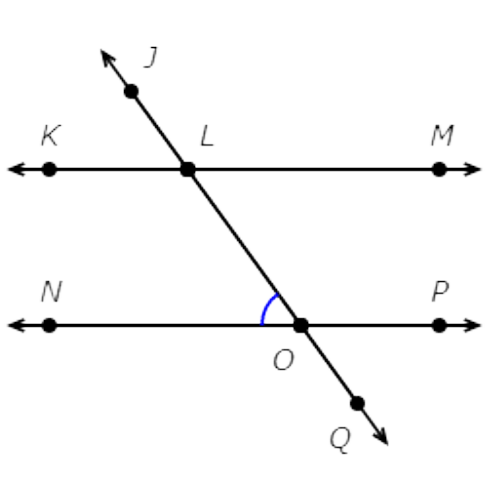
Check each pair of angles.

∠NOL and ∠NOQ are not alternate interior angles. They are on the same side of the transversal.

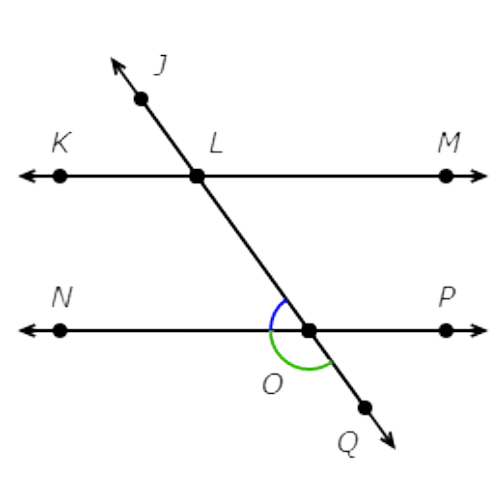
∠NOL and ∠MLO are alternate interior angles.

They are between KM and NP and are on opposite sides of the transversal, but they are not adjacent.

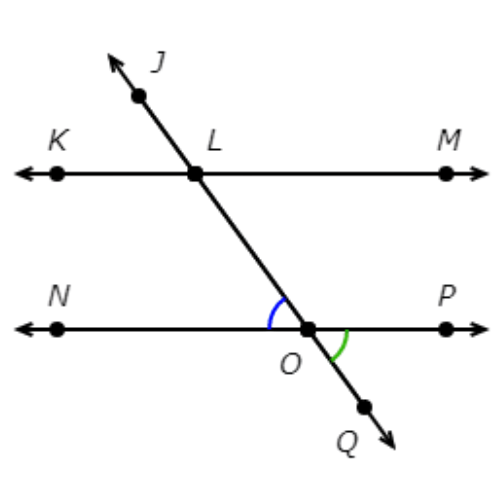
∠NOL and ∠POQ are not alternate interior angles. ∠POQ is not between the parallel lines.

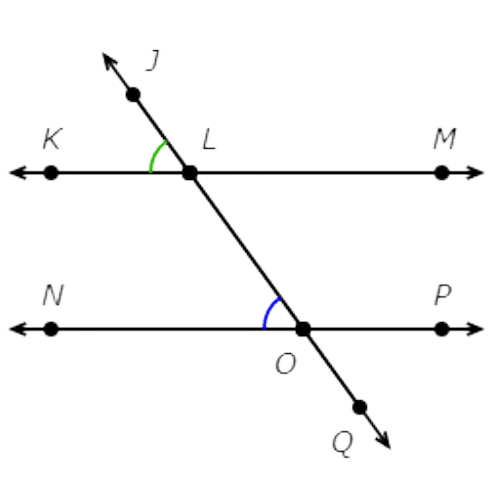
∠NOL and ∠KLJ are not alternate interior angles. They are on the same side of the transversal.

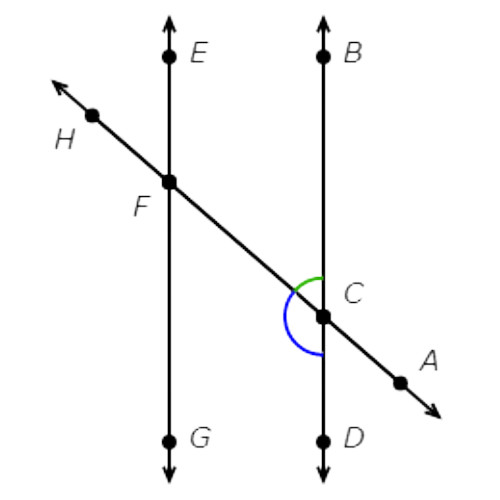
🔔 BD and EG are parallel lines.

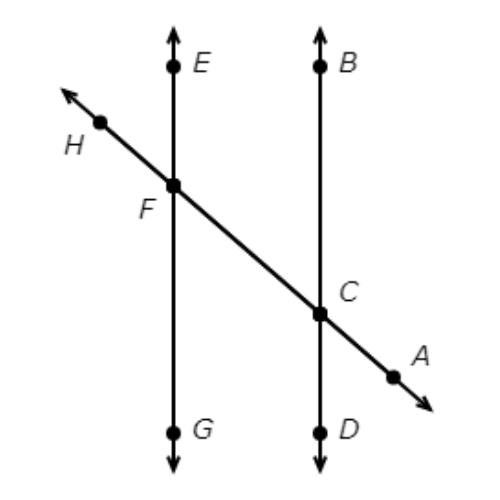
Which angles are adjacent angles?

  • ∠DCF and ∠EFH
  • ∠DCF and ∠BCA
  • ∠DCF and ∠GFH
  • ∠DCF and ∠BCF

First find ∠DCF.

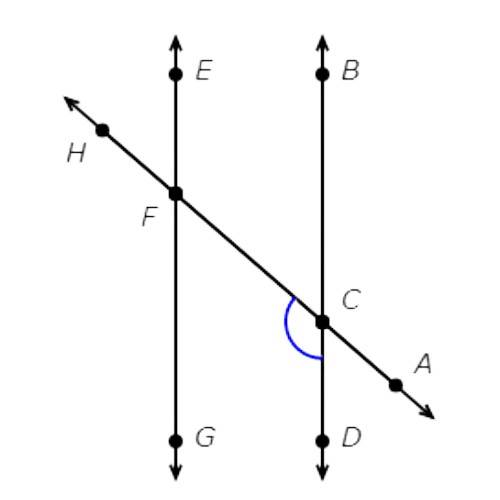
Check each pair of angles.

∠DCF and ∠EFH are not adjacent angles. They do not have a common side.

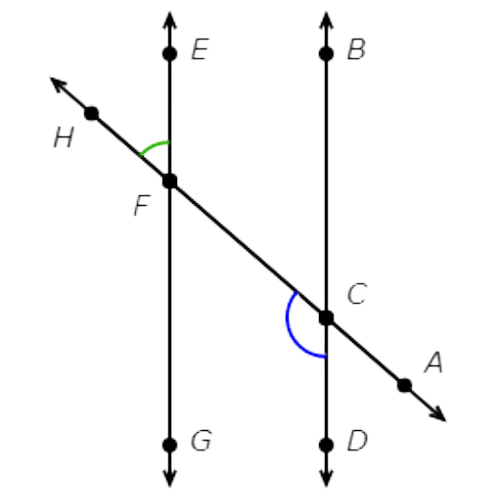
∠DCF and ∠BCA are not adjacent angles. They do not have a common side.

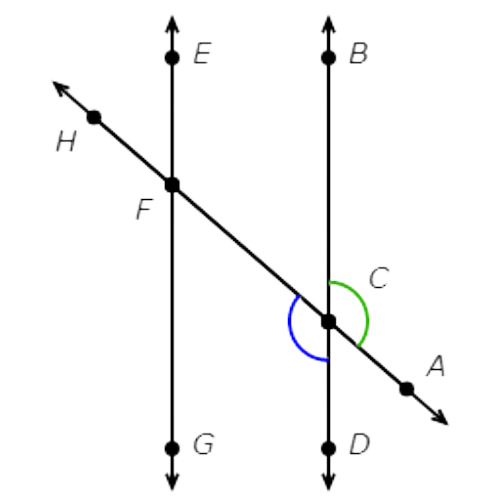
∠DCF and ∠GFH are not adjacent angles. They do not have a common side.

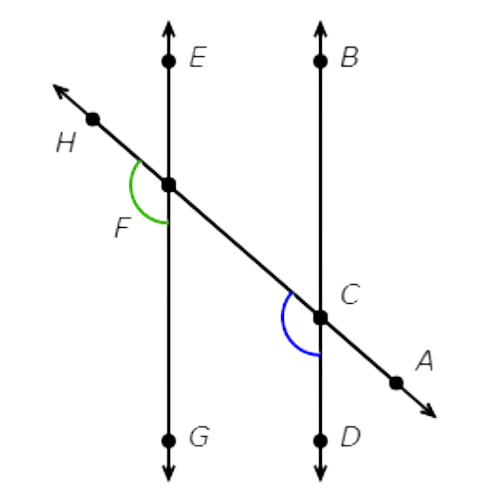
∠DCF and ∠BCF are adjacent angles.

They share the ray CF

🔔 CE and FH are parallel lines.

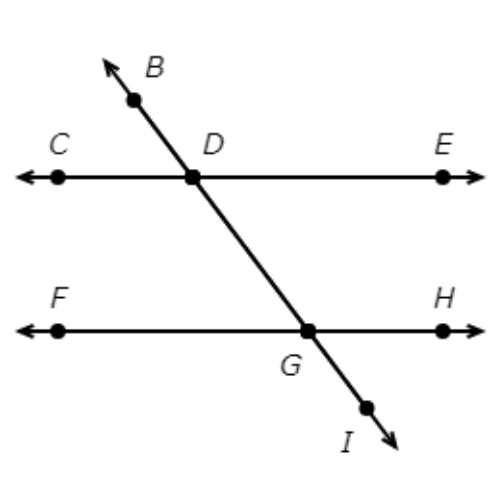
Which angles are adjacent angles?

  • ∠EDB and ∠HGD
  • ∠EDB and ∠CDG
  • ∠EDB and ∠CDB
  • ∠EDB and ∠FGD

First find ∠EDB.

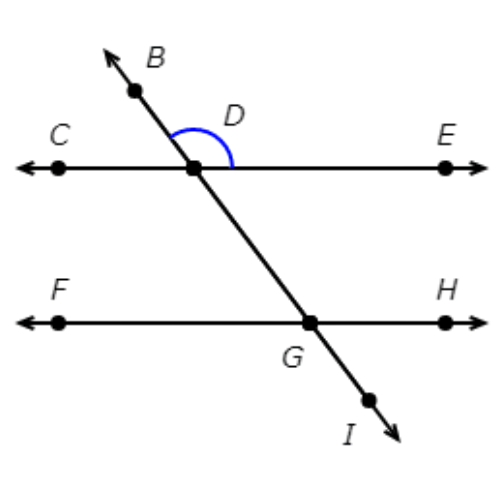
Check each pair of angles.

∠EDB and ∠HGD are not adjacent angles. They do not have a common side.

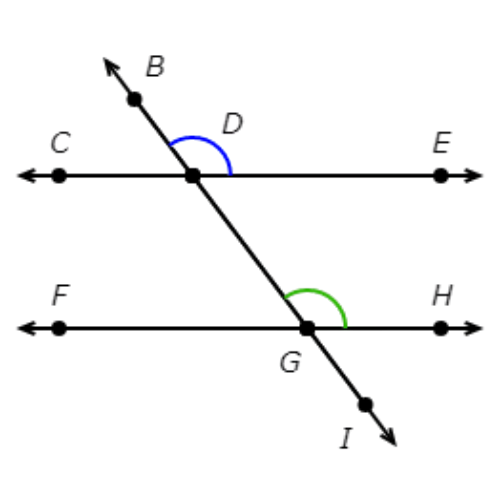
∠EDB and ∠CDG are not adjacent angles. They do not have a common side.

∠EDB and ∠CDB are adjacent angles.

They share the ray DB

∠EDB and ∠FGD are not adjacent angles. They do not have a common side.

Let’s practice!🖊️