Definition: The triangle angle-sum property states that the sum of the interior angles of a triangle is always equal to 180 degrees.

Key Points:

1. Understanding Angles:
   • A triangle has three angles.
   • Each angle is formed by the intersection of two sides of the triangle.
2. Mathematical Representation:
   • If a triangle has angles A, B, and C, then: A+B+C=180^∘
3. Types of Triangles:
   • Acute Triangle: All angles are less than 90 degrees.
   • Right Triangle: One angle is exactly 90 degrees.
   • Obtuse Triangle: One angle is greater than 90 degrees.
4. Applications:
   • This property can be used to find missing angles in a triangle if two angles are known.
   • It is foundational in solving various geometric problems and proofs.

Learn with an example

🌀 The diagram shows a triangle.

What is the value of x?

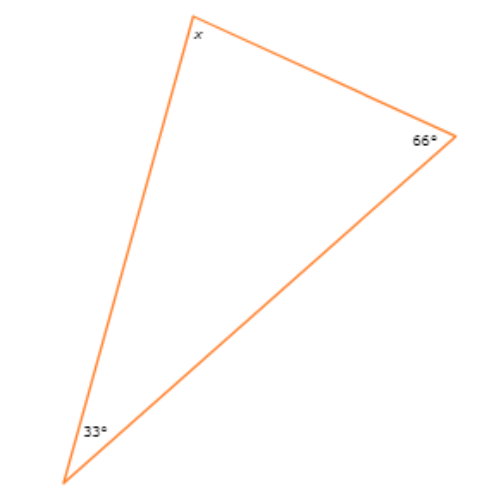
x = _____°

First, look at the interior angle measures in the triangle.

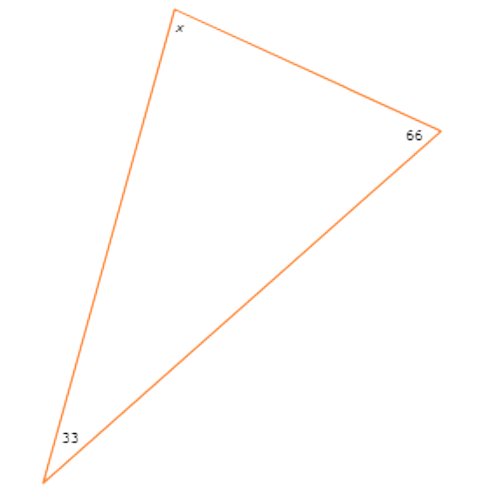
Set the sum of the interior angle measures of the triangle equal to 180°. Solve for x.

33°+x+66°=180°

x+99°=180° Combine like terms

x=81° Subtract 99° from both sides

So, x=81°.

🌀 The diagram shows a triangle.

What is the value of p?

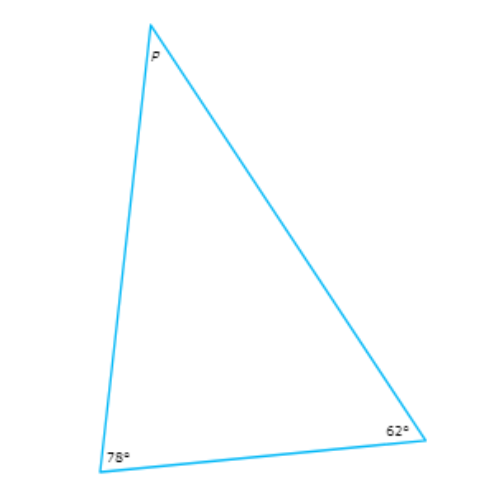
p =_____ °

First, look at the interior angle measures in the triangle.

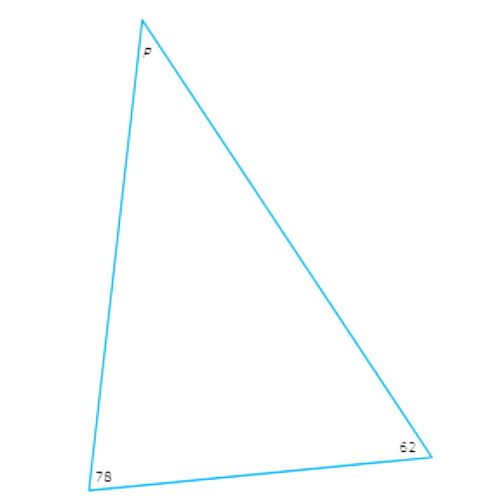
Set the sum of the interior angle measures of the triangle equal to 180°. Solve for p.

78°+p+62°=180°

p+140°=180° Combine like terms

p=40°Subtract 140°  from both sides

So, p=40°.

🌀 The diagram shows a triangle.

What is the value of c?

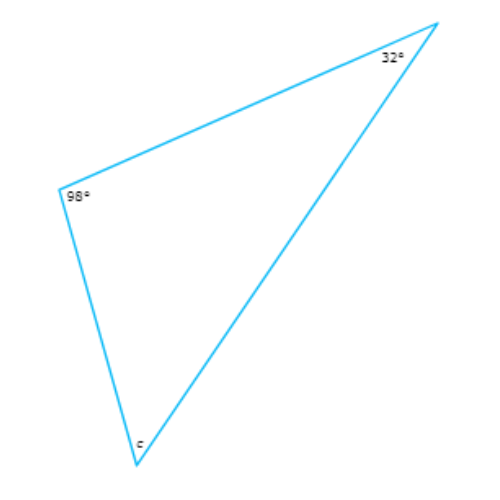
c = ______°

First, look at the interior angle measures in the triangle.

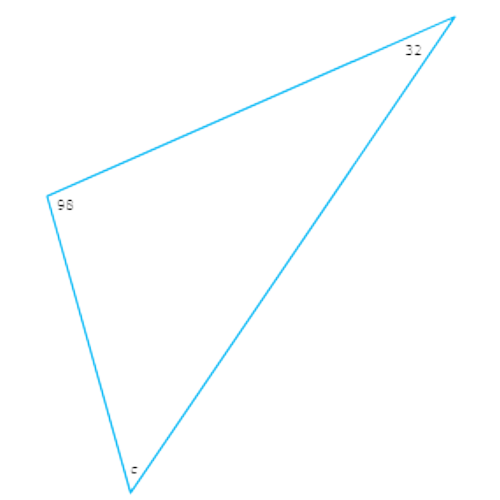
Set the sum of the interior angle measures of the triangle equal to 180°. Solve for c.

32°+c+98°=180°

c+130°=180° Combine like terms

c+130°=180° Combine like terms

So, c=50°.

Let’s practice!🖊️