Exterior angle property
Key notes:
The measure of an exterior angle of a triangle equals the sum of the two remote interior angle measures.
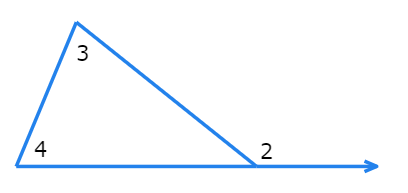
∠2 = ∠3 + ∠4
Exterior Angle Property
- Definition of Exterior Angle:
- An exterior angle is formed when a side of a polygon is extended. It is the angle between the extended side and the adjacent side.
- Exterior Angle Theorem:
- The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
- Mathematically: If ∠D is an exterior angle, then ∠D = ∠A + ∠B (where ∠A and ∠B are the interior angles opposite to the exterior angle).
- Application:
- This property helps in finding unknown angles in triangles, which is useful in solving geometry problems.
- Example: Consider triangle ABC with an exterior angle at vertex C, denoted as angle D. If angle A = 40° and angle B = 60°, then:
∠D = ∠A + ∠B = 40° + 60° = 100°.
Learn with an example
🌀 What is ∠1?
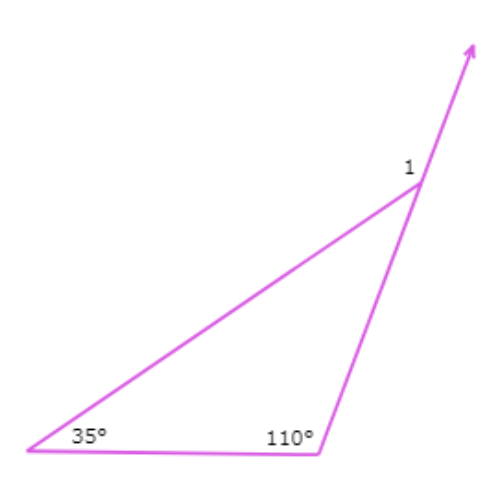
∠1 = _____°
∠1 is an exterior angle of the triangle. The two remote interior angles measure 110° and 35°.
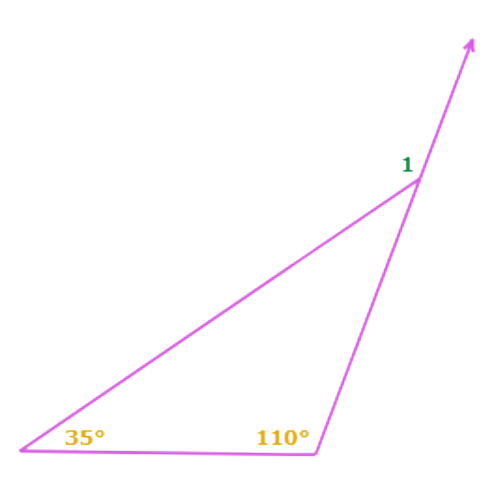
To find the exterior angle measure, add the two remote interior angle measures.
∠1=110°+35°
=145° Add
So, ∠1 = 145°.
🌀 What is ∠1?
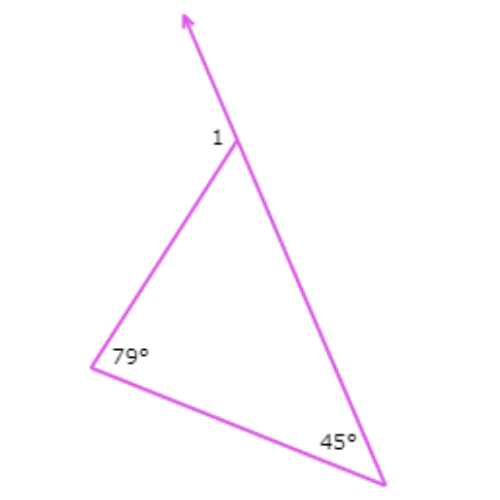
∠1 = ___°
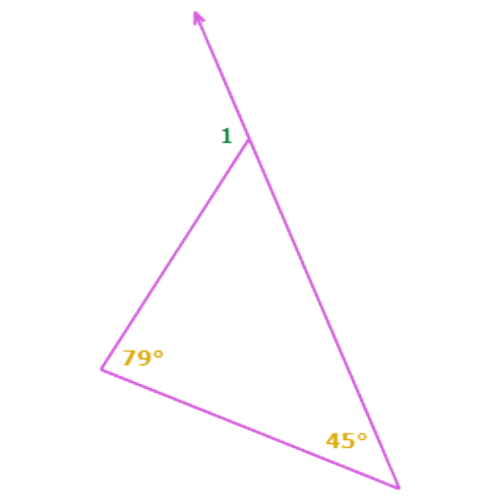
∠1 is an exterior angle of the triangle. The two remote interior angles measure 45° and 79°.
To find the exterior angle measure, add the two remote interior angle measures.
∠1=45°+79°
=124° Add
So, ∠1 = 124°.
🌀 What is ∠1?
∠1 = _______°
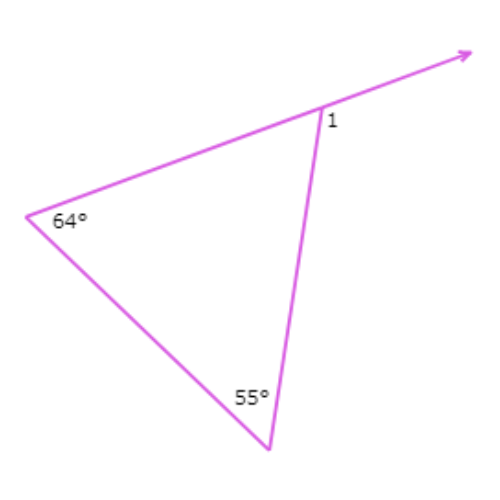
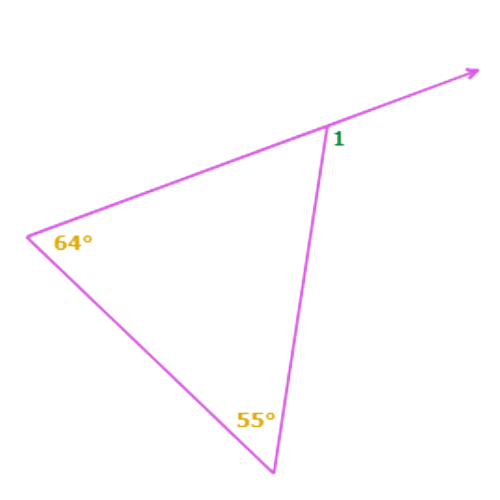
∠1 is an exterior angle of the triangle. The two remote interior angles measure 55° and 64°.
To find the exterior angle measure, add the two remote interior angle measures.
∠1= 55°+64°
= 119° Add
So, ∠1 = 119°.
Let’s practice!🖊️

