Similar and congruent figures
Key notes:
Similar Figures
- Definition: Similar figures have the same shape but may have different sizes. Their corresponding angles are equal, and their corresponding sides are in proportion.
- Notation: If two figures are similar, it is often denoted as △ABC∼△DEF meaning triangle ABC is similar to triangle DEF.
- Scale Factor: The ratio of the lengths of corresponding sides of similar figures is called the scale factor. For example, if the sides of one triangle are twice as long as those of another triangle, the scale factor is 2.
- Angle-Angle (AA) Similarity Postulate: If two angles of one triangle are equal to two angles of another triangle, the two triangles are similar.
- Applications: Similar figures are used in real-life situations, such as in maps, models, and drawings where the scale needs to be maintained.
Congruent Figures
- Definition: Congruent figures have the same shape and size. All corresponding sides and angles are equal.
- Notation: If two figures are congruent, it is denoted as △ABC≅△DEF indicating that triangle ABC is congruent to triangle DEF.
- Criteria for Congruence: Several criteria can determine if triangles are congruent, such as:
- Side-Side-Side (SSS) Congruence: All three pairs of corresponding sides are equal.
- Side-Angle-Side (SAS) Congruence: Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.
- Angle-Side-Angle (ASA) Congruence: Two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
- Transformation: Congruent figures can be obtained through transformations such as translation (sliding), rotation (turning), and reflection (flipping) without changing their size or shape.
- Applications: Congruent figures are used in various fields, including architecture, engineering, and art, to ensure parts fit together perfectly.
Summary
- Similar Figures: Same shape, different size, equal angles, proportional sides.
- Congruent Figures: Same shape and size, equal angles and sides.
Learn with an example
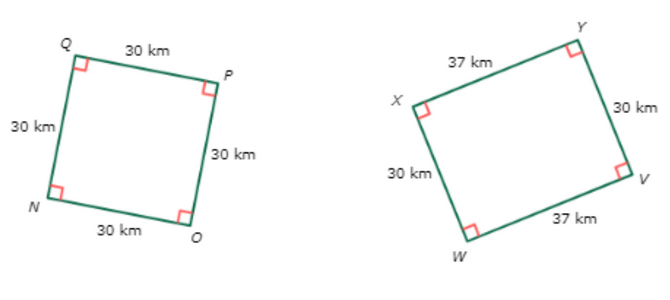
🔔 Are these shapes similar?
- yes
- no
Look for the parts that appear to be corresponding. Reflect the second shape so that it matches the first shape.
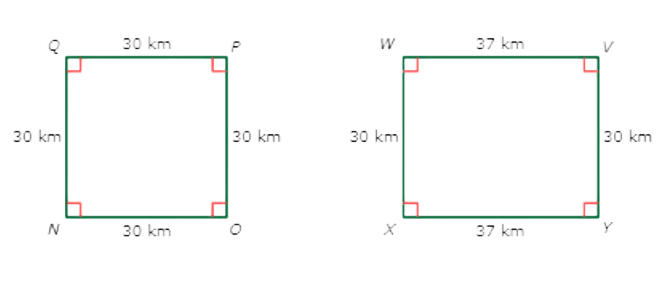
First, see if the corresponding angles are all congruent.
∠N ≅ ∠X
∠O ≅ ∠Y
∠P ≅ ∠V
∠Q ≅ ∠W
The corresponding angles are all congruent.
Next, see if the corresponding sides are proportional. Start by finding the lengths of all the sides.
NO and XY have a ratio of 30/37
OP and YV have a ratio of 30/30 , which is equivalent to 1/1
PQ and VW have a ratio of 30/37 ,
QN and WX have a ratio of 30/30, which is equivalent to 1/1 ,
The ratios are not all the same, so the corresponding sides are not proportional.
Since the corresponding sides are not proportional, the shapes are not similar.
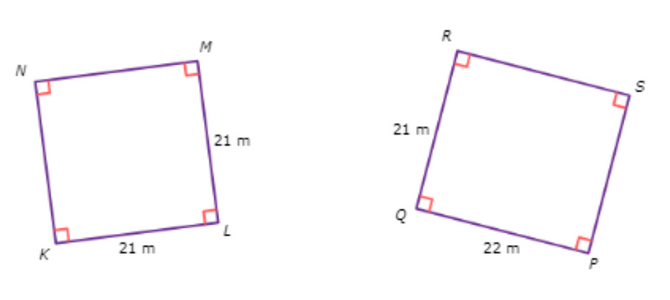
🔔 Are these shapes similar?
- yes
- no
Look for the parts that appear to be corresponding. Reflect the second shape so that it matches the first shape.
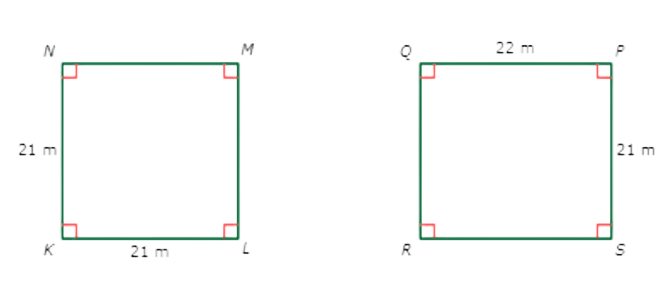
First, see if the corresponding angles are all congruent.
- ∠K ≅ ∠R
- ∠L ≅ ∠S
- ∠M ≅ ∠P
- ∠N ≅ ∠Q
The corresponding angles are all congruent.
Next, see if the corresponding sides are proportional. Start by finding the lengths of all the sides.
KLMN is a square. All the sides are the same length. LM and MN are both 21 m.
RSPQ is a rectangle. The opposite sides are congruent. RS is 22 m and QR is 21 m.
KL and RS have a ratio of 21/22 ,
LM and SP have a ratio of 21/21, which is equivalent to 1/1 ,
MN and PQ have a ratio of 21/22 ,
NK and QR have a ratio of 21/22 , which is equivalent to 1/1 ,
The ratios are not all the same, so the corresponding sides are not proportional.
Since the corresponding sides are not proportional, the shapes are not similar.
🔔 Are these shapes congruent?
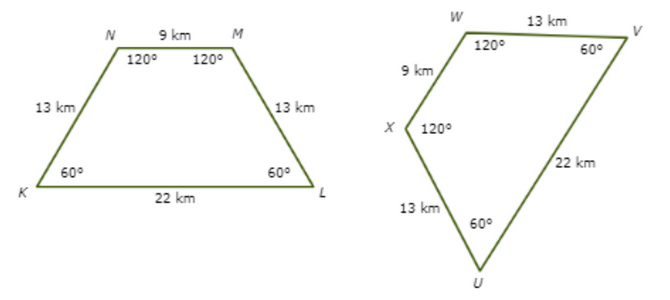
- yes
- no
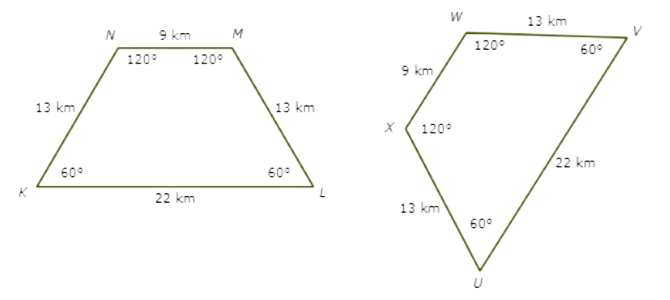
Match up the shapes so that the corresponding angles are congruent.
∠K ≅ ∠U ∠L ≅ ∠V ∠M ≅ ∠W ∠N ≅ ∠X
Next, look at the sides. All the corresponding sides are congruent.

Since there is a correspondence between the shapes such that corresponding angles and sides are congruent, the shapes are congruent.
Let’s practice!🖊️

