Side lengths and angle measures of congruent figures
key notes :
Congruent Figures
- Congruent figures are figures that have the same size and shape.
- Two figures are congruent if they can be placed on top of each other so that they match exactly.
Corresponding Parts
- Corresponding parts of congruent figures are the parts that match up when the figures are placed on top of each other.
- Corresponding sides are equal in length.
- Corresponding angles are equal in measure.
Congruence Statements
- Congruence statements are used to indicate that two figures are congruent.
- For example, if triangle ABC is congruent to triangle DEF, it is written as triangle ABC ≅ triangle DEF.
Properties of Congruent Figures
- If two figures are congruent, their corresponding sides are equal in length.
- If two figures are congruent, their corresponding angles are equal in measure.
- If two figures have all corresponding sides equal in length and all corresponding angles equal in measure, they are congruent.
Learn with an example
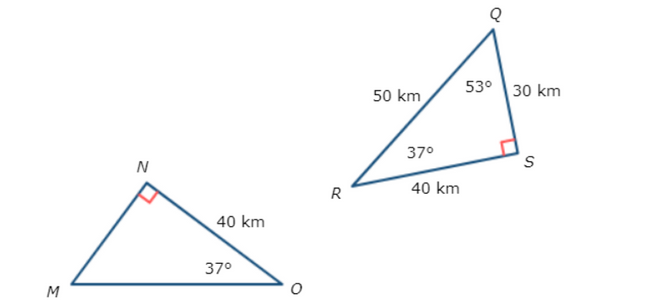
🔔 These figures are congruent. What is MO?
_______ kilometres
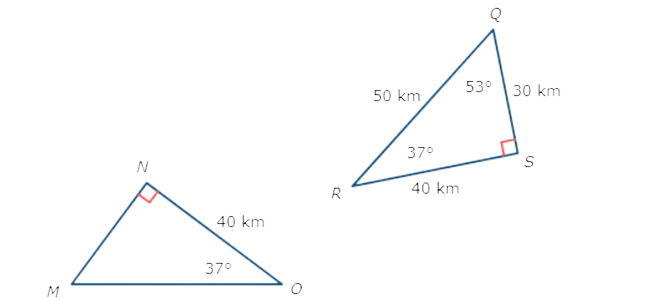
First, write a congruency statement. Remember that corresponding vertices must appear in the same order.
∆MON ≅ ∆QRS
You know that ∆MON ≅ ∆QRS, which means that ∆MON is congruent to ∆QRS. Find the side in ∆QRS that corresponds to ∆MO.
MO ≅ QR
Since MO ≅ QR, the two sides have the same length.
According to the figure, QR = 50 km. So, MO = 50 km.
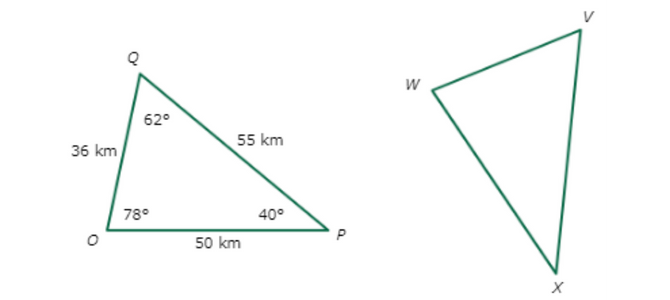
🔔 ∆OPQ ≅ ∆WXV. What is XV?
_______ kilometres
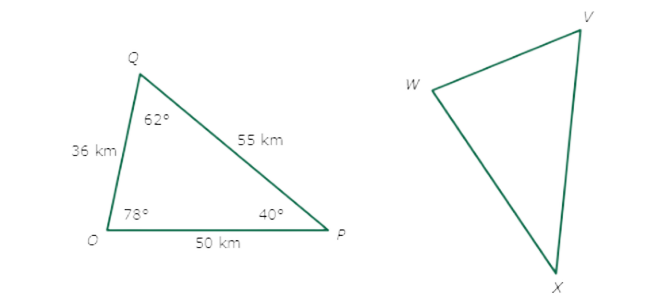
You know that ∆OPQ ≅ ∆WXV, which means that ∆OPQ is congruent to ∆WXV. Find the side in ∆OPQ that corresponds to XV.
XV ≅ PQ
Since XV ≅ PQ, the two sides have the same length.
According to the figure, PQ = 55 km. So, XV = 55 km.
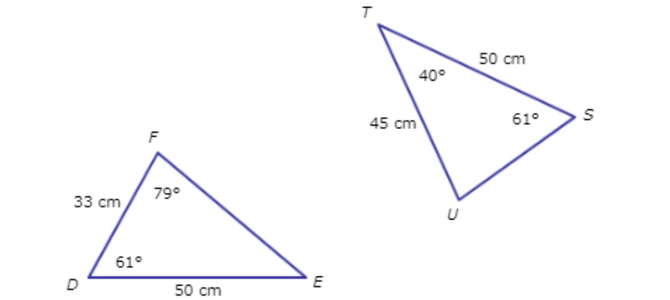
🔔 These figures are congruent. What is U?
_____°
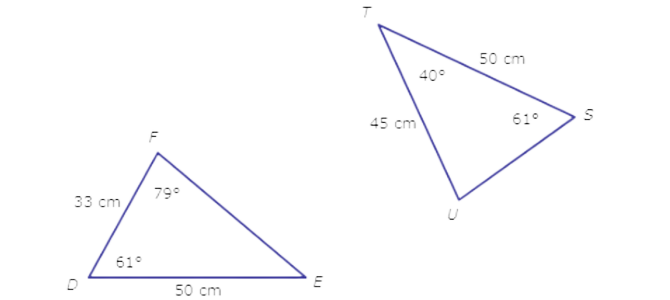
First, write a congruency statement. Remember that corresponding vertices must appear in the same order.
∆DEF ≅ ∆STU
You know that ∆DEF ≅ ∆STU, which means that ∆DEF is congruent to ∆STU. Find the angle in ∆DEF that corresponds to ∠U.
∠U ≅ ∠F
Since ∠U ≅ ∠F, the two angles have the same measure.
According to the figure, ∠F = 79°. So, ∠U = 79°.
Let’s practice!🖊️

