Key notes:

Similar Figures

• Similar figures are figures that have the same shape but not necessarily the same size.
• Two figures are similar if their corresponding angles are congruent and their corresponding sides are in proportion.  

Scale Factor

• The scale factor is the ratio of the corresponding side lengths of two similar figures.
• If the scale factor is greater than 1, the second figure is larger than the first.
• If the scale factor is less than 1, the second figure is smaller than the first.

Properties of Similar Figures

• Corresponding angles of similar figures are congruent.
• Corresponding sides of similar figures are in proportion.  
• The ratio of the perimeters of two similar figures is equal to the scale factor.
• The ratio of the areas of two similar figures is equal to the square of the scale factor.

Key Points to Remember:

• Similar figures have the same shape but not necessarily the same size.
• Corresponding angles of similar figures are congruent.
• Corresponding sides of similar figures are in proportion.  
• The scale factor is the ratio of the corresponding side lengths of two similar figures.

Learn with an example

🔔 If these two shapes are similar, what is the measure of the missing length d?

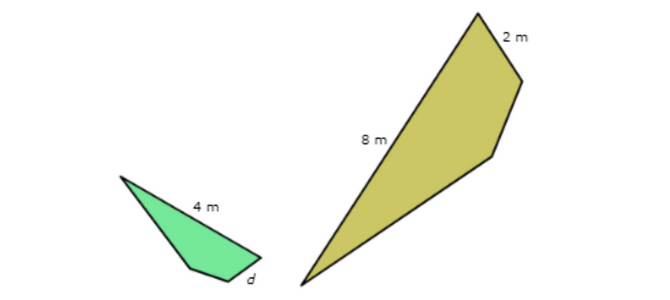
d = ______ metres

Rotate the quadrilaterals to match up the corresponding parts.

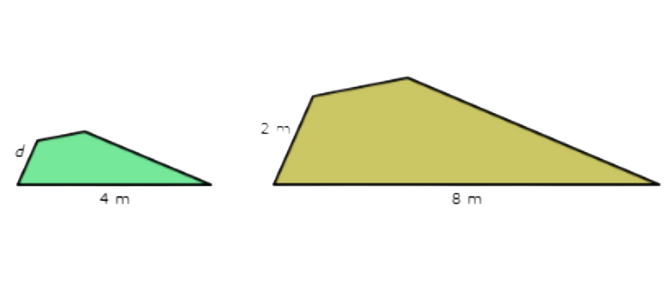
The quadrilaterals’ longer sides have a ratio of  4/8 , which is 1/2

The quadrilaterals’ shorter sides have a ratio of  d/2 ,

Write a proportion:

1/2 = d/2

Multiply both sides by 2 · 2 and solve:

2 = 2d

2 ÷ 2 = 2d ÷ 2

1 = d

The missing length is 1 metre.

🔔 If these two figures are similar, what is the measure of the missing angle?

____°

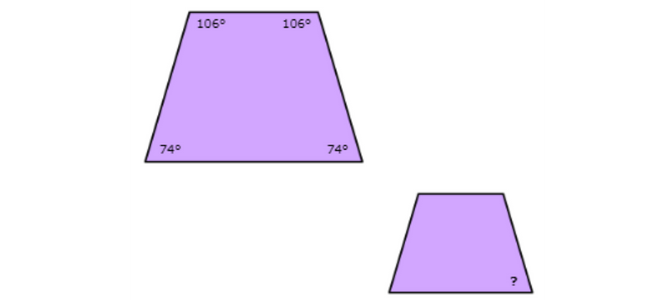
Look at the angle with the question mark. Find the corresponding angle in the other shape.

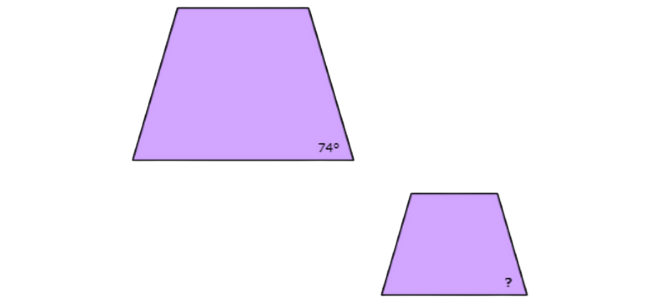
Since the shapes are similar, the measure of the missing angle is also 74°.

🔔 If these two figures are similar, what is the measure of the missing angle?

_____°

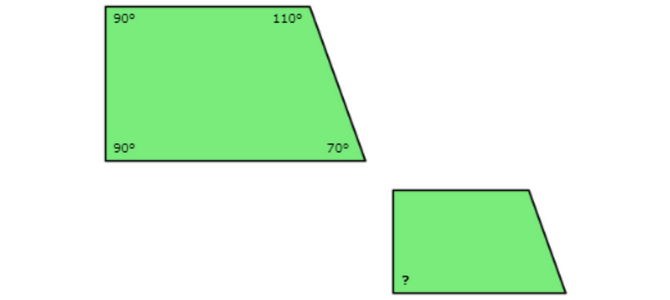
Look at the angle with the question mark. Find the corresponding angle in the other shape.

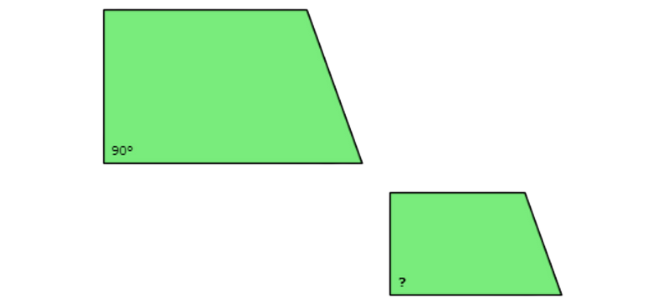
Since the shapes are similar, the measure of the missing angle is also 90°.

Let’s practice!🖊️