Similar figures and indirect measurement
Key notes:
Similar Figures
- Similar figures have the same shape but not necessarily the same size.
- Corresponding angles of similar figures are congruent.
- Corresponding sides of similar figures are in proportion.
- The scale factor is the ratio of the corresponding side lengths of two similar figures.
Indirect Measurement
- Indirect measurement is a technique used to find the length or height of an object without directly measuring it.
- It often involves using similar triangles.
Steps for Indirect Measurement Using Similar Triangles:
- Identify similar triangles: Look for two triangles that have the same shape and corresponding angles.
- Set up a proportion: Write a proportion using the corresponding side lengths of the similar triangles.
- Solve for the missing measurement: Use cross-multiplication or other algebraic methods to solve for the missing measurement.
Key Points to Remember:
- Similar figures have the same shape but not necessarily the same size.
- Indirect measurement uses similar triangles to find unknown measurements.
Learn with an example
🔔 In the diagram below, ∆CDE ∆FGE. Find w.
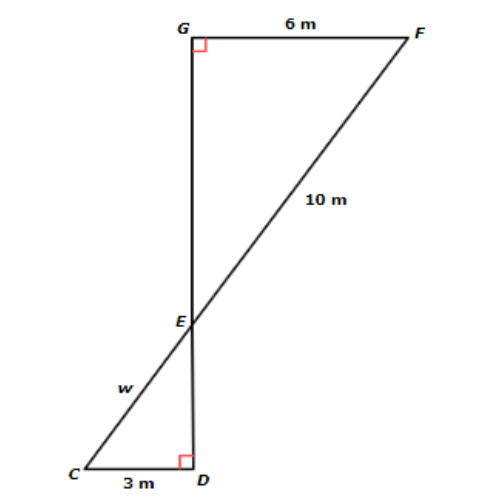
Write your answer as a whole number or a decimal. Do not round.
w =____ metres
The original diagram included a smaller triangle and a larger triangle. Redraw them as separate triangles with corresponding sides in the same colour.
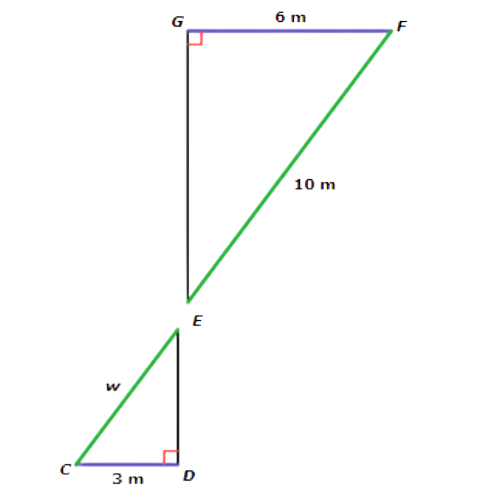
∆CDE ~ ∆FGE means that ∆CDE is similar to ∆FGE.
One pair of corresponding side lengths is FG and CD. Together they form the fraction FG/CD ,
Another pair of corresponding side lengths is EF and EC. Together they form the fraction EF/EC
In both fractions, the numerator comes from ∆FGE and the denominator comes from ∆CDE. Since the triangles are similar, you can use the fractions to set up a proportion and solve for w.
FG/CD = EF/EC
6/3 = 10/W Plug in the side lengths
6/3 (3W) = 10/W (3W) Multiply both sides by 3w
6 w=10 · 3 Simplify
6W = 30 Simplify
6 w ÷ 6 = 30 ÷ 6 Divide both sides by 6
W = 5
The missing length is 5 metres.
🔔 In the diagram below, RQP RON. Find q.
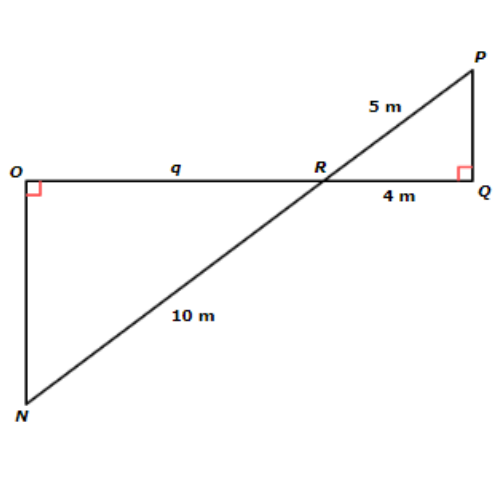
Write your answer as a whole number or a decimal. Do not round.
q = ____ metres
The original diagram included a smaller triangle and a larger triangle. Redraw them as separate triangles with corresponding sides in the same colour.
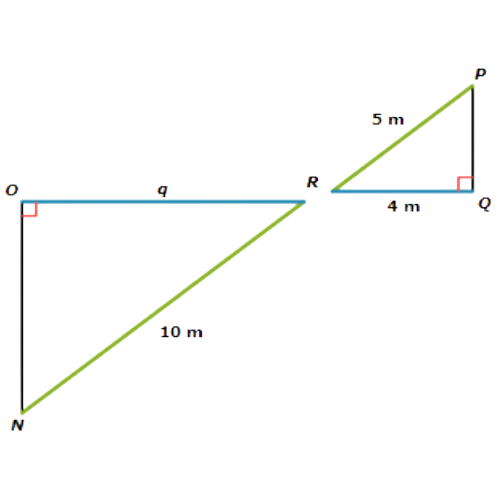
∆RQP ∆RON means that ∆RQP is similar to ∆RON.
One pair of corresponding side lengths is PR and NR. Together they form the fraction PR/NR ,
Another pair of corresponding side lengths is RQ and RO. Together they form the fraction RQ/RO
In both fractions, the numerator comes from RQP and the denominator comes from RON. Since the triangles are similar, you can use the fractions to set up a proportion and solve for q.
PR/NR = RQ/RO
5/10 = 4/q Plug in the side lengths
5/10 (10q) = 4/q (10q) Multiply both sides by 10q
5 q = 4 · 10 Simplify
5q = 40 Simplify
5 q ÷ 5 = 40 ÷ 5 Divide both sides by 5
q = 8
The missing length is 8 metres.
🔔 Find g.
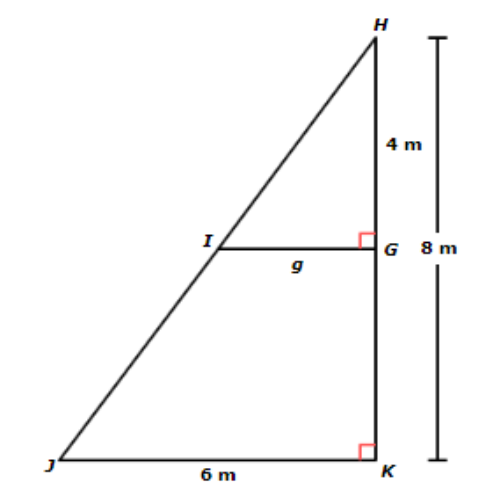
Write your answer as a whole number or a decimal. Do not round.
g = _____ metres
The original diagram included a smaller triangle inside a larger triangle. Redraw them as separate triangles.
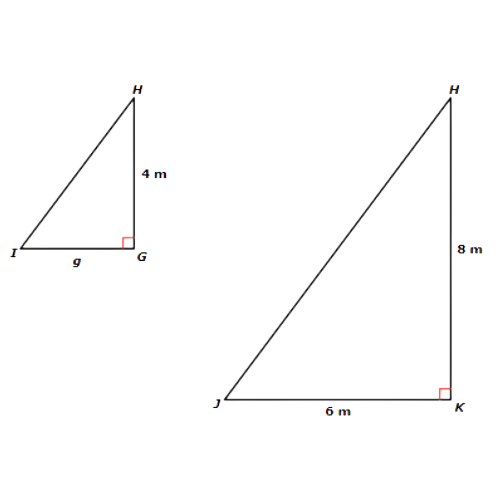
∆GHI is similar to ∆KHJ because all three pairs of corresponding angles are congruent.
One pair of corresponding side lengths is KH and GH. Together they form the fraction KH/GH ,
Another pair of corresponding side lengths is JK and IG. Together they form the fraction JK/IG .
In both fractions, the numerator comes from ∆KHJ and the denominator comes from ∆GHI. Since the triangles are similar, you can use the fractions to set up a proportion and solve for g.
KH/GH = JK/IG
8/4 = 6/g Plug in the side lengths
8/4 (4g) = 6/g (4g) Multiply both sides by 4g
8g = 6.4 Simplify
8g = 24 Simplify
8 g ÷ 8 = 24 ÷ 8 Divide both sides by 8
g = 3
The missing length is 3 metres.
Let’s practice!🖊️

