Perimeter, area and volume: changes in scale
Key Notes :
| 🔹Meaning of Scale |
Scale means enlarging (making bigger) or reducing (making smaller) a shape while keeping the same proportions.
When dimensions (length, width, height) of a figure are multiplied by a scale factor, its perimeter, area, and volume also change.
| 🔹Effect of Scale Factor on Perimeter, Area, and Volume |
👉 Suppose the scale factor = k
(Every length is multiplied by k)
Perimeter (1-D Measurement)
- Perimeter is directly proportional to the scale factor.
- New Perimeter = k × Original Perimeter
Area (2-D Measurement)
- Area is proportional to the square of the scale factor.
- New Area = k² × Original Area
Volume (3-D Measurement)
- Volume is proportional to the cube of the scale factor.
- New Volume = k³ × Original Volume
| 🔹 Examples |
Example 1: Perimeter
- A square has side = 5 cm.
- Scale factor = 3.
- New side = 5 × 3 = 15 cm.
- Original Perimeter = 4 × 5 = 20 cm.
- New Perimeter = 3 × 20 = 60 cm. ✅
Example 2: Area
- Rectangle = 6 cm × 4 cm.
- Scale factor = 2.
- New dimensions = 12 cm × 8 cm.
- Original Area = 6 × 4 = 24 cm².
- New Area = 2² × 24 = 4 × 24 = 96 cm². ✅
Example 3: Volume
- Cube with side = 2 cm.
- Scale factor = 3.
- New side = 6 cm.
- Original Volume = 2³ = 8 cm³.
- New Volume = 3³ × 8 = 27 × 8 = 216 cm³. ✅
| 🔹Key Points to Remember |
- Perimeter → multiplies by k
- Area → multiplies by k²
- Volume → multiplies by k³
- As shapes grow larger, area and volume grow much faster than perimeter.
| 🔹 Real-Life Applications |
- Maps (scale drawings).
- Models of buildings, cars, and machines.
- Enlarging/reducing images in printing or designing.
| ✅ Summary: |
When a figure is enlarged or reduced by a scale factor (k):
- Perimeter × k
- Area × k²
- Volume × k³
Learn with an example
▶️ Look at this rectangular prism:
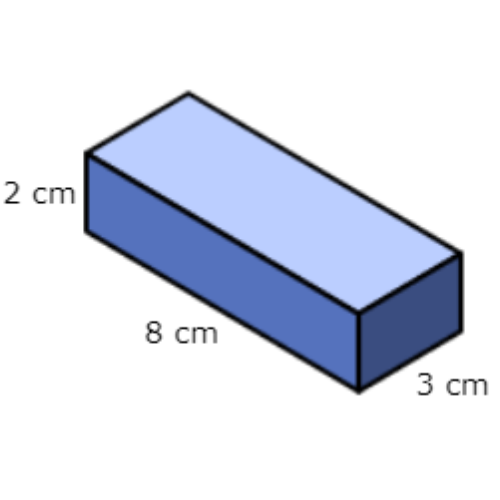
If the width is doubled, then which of the following statements about its volume will be true?
Look at this rectangular prism:
- The new volume will be 3 times the old volume.
- The new volume will be 2 times the old volume.
- The new volume will be 12 of the old volume.
- The new volume will be 4 times the old volume.
You can solve this problem without using the measurements given in the diagram.
The original rectangular prism had this volume:
V = lwh
The new rectangular prism will have 2 times the width. Since the original width was w, the new width will be 2w. Calculate the volume:
V = l(2w)h
= 2lwh
Divide the new volume by the original volume and simplify.
new volume/ original volume = 2lwh / lwh
= 2
The new volume will be 2 times the old volume.
▶️ Look at this cube:
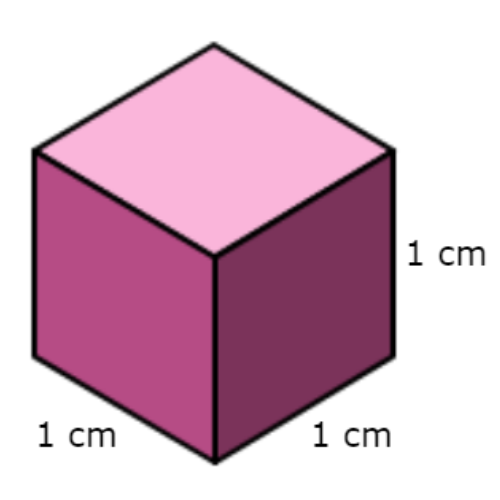
If the side lengths are tripled, then which of the following statements about its surface area will be true?
- The new surface area will be 3 times the old surface area
- The new surface area will be 1/4 of the old surface area
- The new surface area will be 27 times the old surface area.
- The new surface area will be 9 times the old surface area
You can solve this problem without using the measurements given in the diagram.
The original cube had this surface area:
S = 6s2
The new cube will have sides that are 3 times as long. Since the original side lengths were s, the new side lengths will be 3s. Calculate the surface area:
S = 6(3s)2
= 6 · 9s2
= 54s2
Divide the new surface area by the original surface area and simplify.
new surface area / original surface area = 54s2 / 6s2
= 9
The new surface area will be 9 times the old surface area.
▶️ Look at this square:
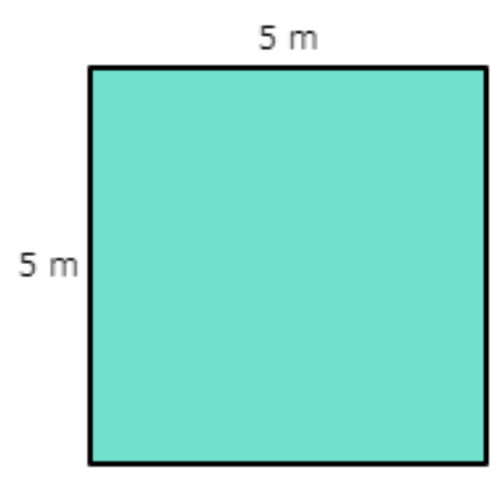
If the side lengths are doubled, then which of the following statements about its perimeter will be true?
- The new perimeter will be 2 times the old perimeter.
- The new perimeter will be 3 times the old perimeter.
- The new perimeter will be 1/2 of the old perimeter.
- The new perimeter will be 4 times the old perimeter.
You can solve this problem without using the measurements given in the diagram.
The original square had this perimeter:
P = 4s
The new square will have sides that are 2 times as long. Since the original side lengths were s, the new side lengths will be 2s. Calculate the perimeter:
P = 4(2s)
= 8s
Divide the new perimeter by the original perimeter and simplify.
new perimeter / original perimeter = 8s/4s
= 2
The new perimeter will be 2 times the old perimeter.
Let’s practice!🖊️

