Area of compound figures with triangles, semicircles and quarter circles
Key Notes :
| 🔹What are Compound Figures? |
- A compound figure (or composite figure) is a shape made up of two or more simple shapes.
- Examples of simple shapes: triangle, square, rectangle, circle, semicircle, quarter circle, trapezium.
- To find the area of a compound figure, we divide it into known shapes, calculate each area, and then add or subtract as needed.
| 🔹 Area Formulas to Remember |
- Triangle: Area=1/2×base×height
- Circle: Area=πr2
- Semicircle (half circle): Area=1/2πr2
- Quarter Circle (one-fourth of circle): Area=1/4πr2
| 🔹Steps to Solve Compound Figures |
- Identify the shapes inside the figure.
- Divide the figure into known shapes (triangle, semicircle, quarter circle, etc.).
- Apply the correct area formulas for each part.
- Add areas if shapes are joined together.
- Subtract areas if a part is removed or cut out.
| 🔹 Example Problems |
✨ Example 1: Triangle + Semicircle
A figure has a triangle of base 10 cm and height 6 cm. A semicircle of radius 5 cm is attached to one side of the triangle.
- Area of triangle = 1/2×10×6=30 cm2
- Area of semicircle = 1/2π(52)=1/2×3.14×25=39.25 cm2
- Total area = 30+39.25=69.25 cm2
✨ Example 2: Square with Quarter Circles in Corners
A square of side 14 cm has quarter circles drawn in each corner (radius 7 cm). Find the area left inside the square.
- Area of square = 14×14=196 cm2
- Area of one quarter circle = 1/4π(72)=14×3.14×49=38.465 cm2
- 4 quarter circles = 4×38.465=153.86 cm2
- Remaining area = 196−153.86=42.14 cm2
| ✨ Key Points to Remember |
- Always draw and label the figure clearly.
- Use the correct radius (r) for circles and base, height for triangles.
- Add areas when shapes are combined.
- Subtract areas when a part is cut out.
- Use π = 3.14 (or 22/7) depending on the question.
Learn with an example
▶️ What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋. square
_______ centimetres
Divide the figure into separate shapes:
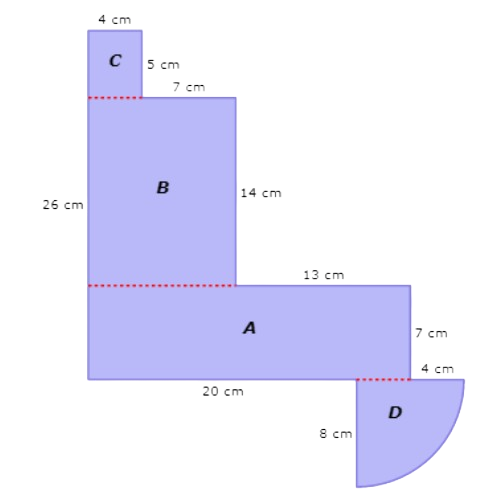
Start with rectangle A. Rectangle A is 24 centimetres wide and 7 centimetres tall.
Multiply:
24 . 7 = 168
The area of rectangle A is 168 cm2.
Look at rectangle C. Rectangle C is 4 centimetres wide and 5 centimetres tall.
Multiply:
4 . 5 = 20
The area of rectangle C is 20 cm2.
Look at quarter circle D. Quarter circle D has a radius of 8 centimetres.
Solve for the area of quarter circle D.
3.14 . 82 / 4 = 50 . 24
The area of quarter circle D is 50.24 cm2.
Now add the areas of all the shapes.
168 cm2 + 154 cm2 + 20 cm2 + 50.24 cm2 = 392.24 cm2
The area is 392.24 square centimetres.
▶️ What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋. square
______ millimetres
Divide the figure into separate shapes:
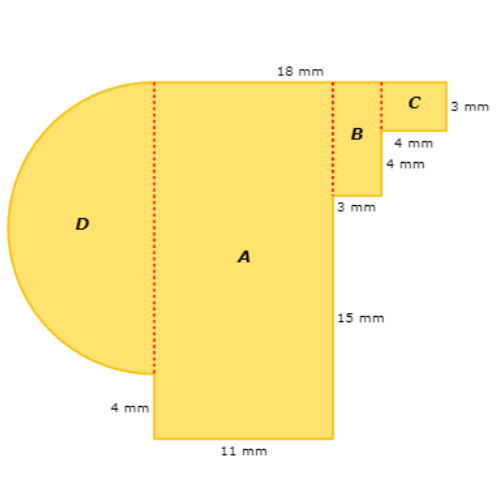
Start with rectangle A. Rectangle A is 11 millimetres wide and 22 millimetres tall.
Multiply:
11 . 22 = 242
The area of rectangle A is 242 mm2.
Look at rectangle B. Rectangle B is 3 millimetres wide and 7 millimetres tall.
Multiply:
3. 7 = 21
The area of rectangle B is 21 mm2.
Look at rectangle C. Rectangle C is 4 millimetres wide and 3 millimetres tall.
Multiply:
4 . 3 = 12
The area of rectangle C is 12 mm2.
Look at semicircle D. Semicircle D has a diameter of 18 millimetres, which gives it a radius of 9 millimetres.
Solve for the area of semicircle D.
3 . 14 . 92 / 2 = = 127.17
The area of semicircle D is 127.17 mm2.
Now add the areas of all the shapes.
242 mm2 + 21 mm2 + 12 mm2 + 127.17 mm2 = 402.17 mm2
The area is 402.17 square millimetres.
▶️ What is the area of this figure?

Write your answer using decimals. Use 3.14 for 𝜋.
________ square kilometres
Divide the figure into separate shapes:
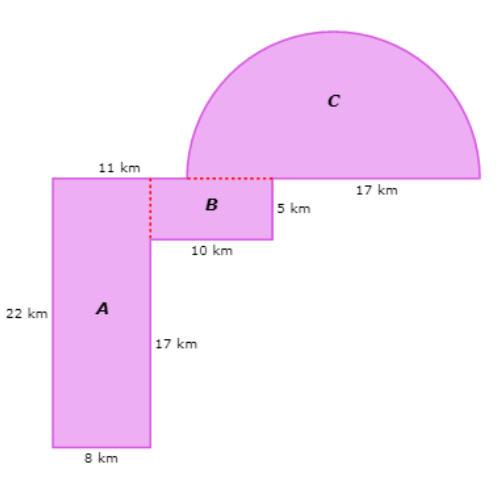
Start with rectangle A. Rectangle A is 8 kilometres wide and 22 kilometres tall.
Multiply:
8 . 22 = 176
The area of rectangle A is 176 km2.
Look at rectangle B. Rectangle B is 10 kilometres wide and 5 kilometres tall.
Multiply:
10 . 5 = 50
The area of rectangle B is 50 km2.
Look at semicircle C. Semicircle C has a diameter of 24 kilometres, which gives it a radius of 12 kilometres.
Solve for the area of semicircle C.
3.14 . 122 / 2 = 226.08
The area of semicircle C is 226.08 km2.
Now add the areas of all the shapes.
176 km2 + 50 km2 + 226.08 km2 = 452.08 km2
The area is 452.08 square kilometres.
Let’s practice!🖊️

